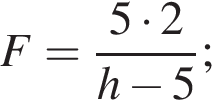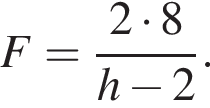На рисунке представлен график зависимости координаты велосипедиста от времени его движения. Начальная координата х0 велосипедиста равна:
На рисунке точками обозначены положения частиц и стрелками показаны скорости их движения в некоторый момент времени. Если все частицы движутся равномерно и прямолинейно, то с частицей А столкнётся частица, обозначенная цифрой:
Примечание. Повторные столкновения частиц не рассматривать.
На рисунке приведён график зависимости пути s, пройденного телом при прямолинейном движении с постоянным ускорением, от времени t. Модуль ускорения a тела равен:
Абсолютное удлинение ![]() первой пружины в два раза больше абсолютного удлинения
первой пружины в два раза больше абсолютного удлинения ![]() второй пружины. Если потенциальные энергии упругой деформации этих пружин равны (EП1 = EП2), то отношение жесткости второй пружины к жесткости первой пружины
второй пружины. Если потенциальные энергии упругой деформации этих пружин равны (EП1 = EП2), то отношение жесткости второй пружины к жесткости первой пружины ![]() равно:
равно:
К некоторому телу приложены силы ![]() и
и ![]() лежащие в плоскости рисунка (см. рис. 1). На рисунке 2 направление ускорения
лежащие в плоскости рисунка (см. рис. 1). На рисунке 2 направление ускорения ![]() этого тела обозначено цифрой:
этого тела обозначено цифрой:
В двух вертикальных сообщающихся сосудах находится ртуть (![]() 1 = 13,6 г/см3). Поверх ртути в один сосуд налили слой воды (
1 = 13,6 г/см3). Поверх ртути в один сосуд налили слой воды (![]() 2 = 1,00 г/см3) высотой H = 20 см. Разность Δh уровней ртути в сосудах равна:
2 = 1,00 г/см3) высотой H = 20 см. Разность Δh уровней ртути в сосудах равна:
На наружной стороне окна висит термометр, показания которого представлены на рисунке. Абсолютная температура Т воздуха за окном равна:
С идеальным газом, количество вещества которого постоянно, провели процесс AB, показанный в координатах (p, T). Этот же процесс в координатах (T, V) изображён на графике, обозначенном цифрой:
| 1 | 2 | 3 | 4 | 5 |
С идеальным одноатомным газом, количество вещества которого постоянно, провели процесс 1→2→3→4→5→1. На рисунке показана зависимость внутренней энергии U газа от объема V. Укажите участок, на котором количество теплоты, полученное газом, шло только на работу, которую газ совершал:
Физической величиной, измеряемой в джоулях, является:
Материальная точка массой m = 2,0 кг движется вдоль оси Ox. График зависимости проекции скорости υx материальной точки на эту ось от времени t представлен на рисунке. В момент времени t = 3 c модуль результирующей всех сил F, приложенных к материальной точке, равен ... H.
На горизонтальной поверхности лежит однородный шар диаметром D = 1,0 м и массой m1 = 1,0 т. Над центром шара расположено небольшое тело на высоте H = 1,5 м от горизонтальной поверхности (см. рис.). Если модуль силы гравитационного притяжения, действующей на тело со стороны шара, F = 1,4 мкН, то масса m2 тела равна ... кг.
На горизонтальном прямолинейном участке сухой асфальтированной дороги водитель применил экстренное торможение. Тормозной путь автомобиля до полной остановки составил 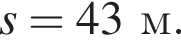 Если коэффициент трения скольжения между колесами и асфальтом
Если коэффициент трения скольжения между колесами и асфальтом 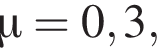 то модуль скорости υ0 движения автомобиля в начале тормозного пути равен ...
то модуль скорости υ0 движения автомобиля в начале тормозного пути равен ... ![]()
Автомобиль движется по дороге со скоростью, модуль которой 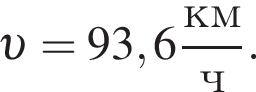 Профиль дороги показан на рисунке. В точке С радиус кривизны профиля R = 255 м. Если в точке С, направление на которую из центра кривизны составляет с вертикалью угол
Профиль дороги показан на рисунке. В точке С радиус кривизны профиля R = 255 м. Если в точке С, направление на которую из центра кривизны составляет с вертикалью угол  модуль силы давления автомобиля на дорогу F = 5,16 кН, то масса m автомобиля равна ... кг.
модуль силы давления автомобиля на дорогу F = 5,16 кН, то масса m автомобиля равна ... кг.
В баллоне находится идеальный газ массой m1 = 700 г. После того как из баллона выпустили некоторую массу газа и понизили абсолютную температуру оставшегося газа так, что она стала на α = 20,0 % меньше первоначальной, давление газа в баллоне уменьшилось на β = 40,0 %. Масса m2 газа в конечном состоянии равна ... г.
Воздух (c = 1 кДж/(кг · °C)) при прохождении через электрический фен нагревается от температуры t1 = 20 °C до t2 = 60 °C. Если мощность, потребляемая феном, P = 1,0 кВт, то масса m воздуха, проходящего через фен за промежуток времени τ = 10 мин, равна ... кг.
Цилиндрический сосуд с идеальным одноатомным газом, закрытый невесомым легкоподвижным поршнем с площадью поперечного сечения S = 240 см2, находится в воздухе, давление которого p0 = 100 кПа. Если при медленном нагревании газа поршень сместился на расстояние l = 70,0 мм, то газу сообщили количество теплоты Q, равное ... Дж.
При изохорном нагревании идеального газа, количество вещества которого постоянно, температура газа увеличилась на ΔT = 160 K, а давление газа увеличилось в k = 1,50 раза. Начальная температура T1 газа была равна ... K.
Если точечный заряд 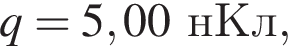 находящийся в вакууме, помещен в точку A (см.рис.), то потенциал электростатического поля, созданного этим зарядом, в точке B равен ... В.
находящийся в вакууме, помещен в точку A (см.рис.), то потенциал электростатического поля, созданного этим зарядом, в точке B равен ... В.
>
Два иона (1 и 2) с одинаковыми заряди  вылетевшие одновременно из точки O, равномерно движутся по окружностям под действием однородного магнитного поля, линии индукции
вылетевшие одновременно из точки O, равномерно движутся по окружностям под действием однородного магнитного поля, линии индукции ![]() которого перпендикулярны плоскости рисунка. На рисунке показаны траектории этих частиц в некоторый момент времени t1. Если масса первой частицы
которого перпендикулярны плоскости рисунка. На рисунке показаны траектории этих частиц в некоторый момент времени t1. Если масса первой частицы 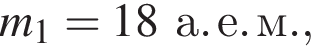 то масса второй частицы m2 равна ... а. е. м.
то масса второй частицы m2 равна ... а. е. м.
Квадратная рамка изготовлена из тонкой однородной проволоки. Сопротивление рамки, измеренное между точками А и В (см. рис.), RAB = 1,0 Ом. Если рамку поместить в магнитное поле, то при равномерном изменении магнитного потока от Ф1 = 39 мВб до Ф2 = 15 мВб через поверхность, ограниченную рамкой, за время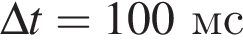 сила тока I в рамке будет равна ... мА.
сила тока I в рамке будет равна ... мА.
Две вертикальные однородно заряженные непроводящие пластины расположены в вакууме на расстоянии d = 40 мм друг от друга. Между пластинами на длинной лёгкой нерастяжимой нити подвешен небольшой заряженный (|q0| = 100 пКл) шарик массой m = 720 мг, который движется, поочерёдно ударяясь о пластины. При ударе о каждую из пластин шарик теряет ![]() = 36,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 400 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
= 36,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 400 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
Стрелка AB высотой H = 3,0 см и её изображение A1B1 высотой h = 2,0 см,формируемое тонкой линзой, перпендикулярны главной оптической оси N1N2 линзы (см. рис.). Если расстояние между стрелкой и её изображением AA1 = 7,0 см, то модуль фокусного расстояния |F| линзы равен ... см.
Для исследования лимфотока пациенту ввели препарат, содержащий N0 = 120 000 ядер радиоактивного изотопа золота ![]() Если период полураспада этого изотопа
Если период полураспада этого изотопа 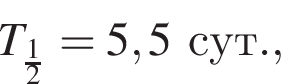 то
то  ядер
ядер ![]() распадётся за промежуток времени
распадётся за промежуток времени ![]() равный ... сут.
равный ... сут.
Если за время Δt = 30 суток показания счётчика электроэнергии в квартире увеличились на ΔW = 31,7 кВт · ч, то средняя мощность P, потребляемая электроприборами в квартире, равна ... Вт.
Электрическая цепь состоит из источника тока, внутреннее сопротивление которого r = 0,50 Ом, и резистора сопротивлением R = 10 Ом. Если сила тока в цепи I = 2,0 А, то ЭДС ℰ источника тока равна ... В.
На рисунке изображена схема электрической цепи, состоящей из источника тока и шести одинаковых резисторов
R1 = R2 = R3 = R4 = R5 = R6 = 10,0 Ом.
В резисторе R6 выделяется тепловая мощность P6 = 90,0 Вт. Если внутреннее сопротивление источника тока r = 4,00 Ом, то ЭДС ℰ источника тока равна ... В.
Электрон, модуль скорости которого 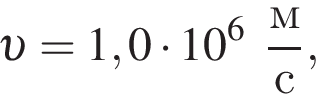 движется по окружности в однородном магнитном поле. Если на электрон действует сила Лоренца, модуль которой
движется по окружности в однородном магнитном поле. Если на электрон действует сила Лоренца, модуль которой 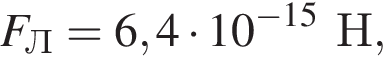 то модуль индукции B магнитного поля равен ... мТл.
то модуль индукции B магнитного поля равен ... мТл.
В идеальном колебательном контуре, состоящем из конденсатора и катушки, индуктивность которой L = 0,20 мГн, происходят свободные электромагнитные колебания. Если циклическая частота электромагнитных колебаний 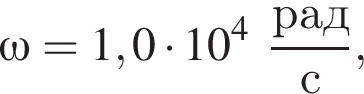 то ёмкость C конденсатора равна ... мкФ.
то ёмкость C конденсатора равна ... мкФ.
График зависимости высоты Н изображения карандаша, полученного с помощью тонкой рассеивающей линзы, от расстояния d между линзой и карандашом показан на рисунке. Модуль фокусного расстояния |F| рассеивающей линзы равен ... дм.
Примечание. Карандаш расположен перпендикулярно главной оптической оси линзы.

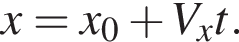
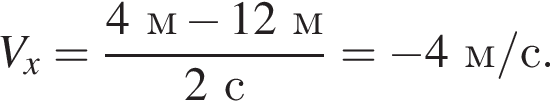
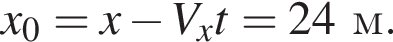
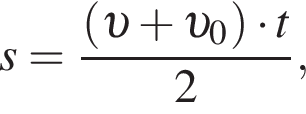 откуда
откуда 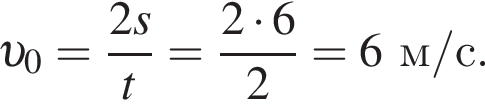 Откуда ускорение равняется
Откуда ускорение равняется 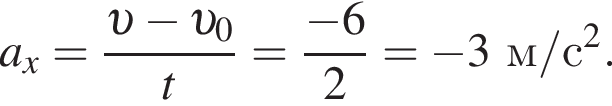
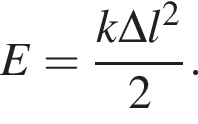 По условию
По условию 
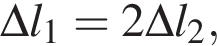 значит
значит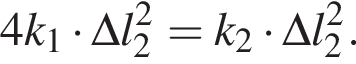
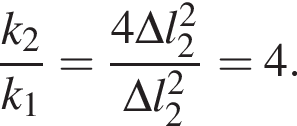

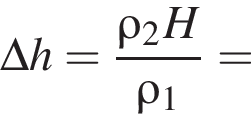

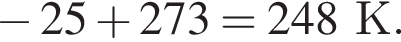
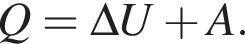 Для того чтобы всё количество теплоты шло только на работу, которую газ совершал, где работа газа
Для того чтобы всё количество теплоты шло только на работу, которую газ совершал, где работа газа 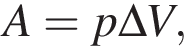 внутренняя энергия должна равняться нулю. На графике такой участок 1→2.
внутренняя энергия должна равняться нулю. На графике такой участок 1→2.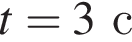 скорость изменялась на 2 м/с за каждую секунду, т. е. ускорение точки было
скорость изменялась на 2 м/с за каждую секунду, т. е. ускорение точки было 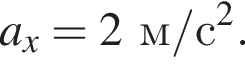 Модуль результирующей всех сил, приложенных к точке, по второму закону Ньютона равен
Модуль результирующей всех сил, приложенных к точке, по второму закону Ньютона равен 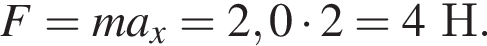
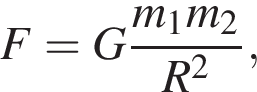 где
где 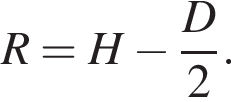 Тогда масса второго тела равна
Тогда масса второго тела равна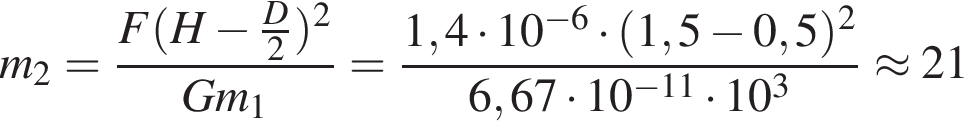
 На горизонтальной поверхности модуль ускорения, возникающий из-за силы трения, равен
На горизонтальной поверхности модуль ускорения, возникающий из-за силы трения, равен 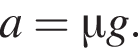 Таким образом,
Таким образом, 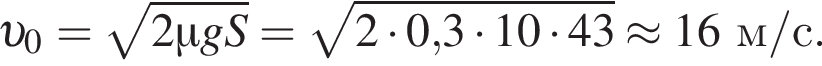
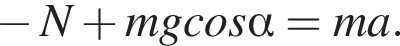 Центростремительное ускорение равно:
Центростремительное ускорение равно: 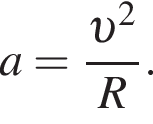 N = F по третьему закону Ньютона.
N = F по третьему закону Ньютона.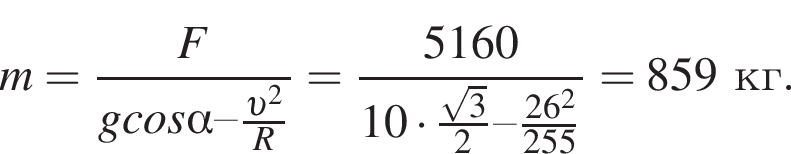
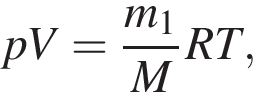
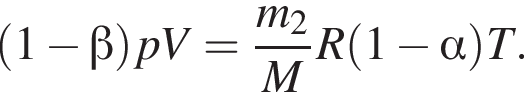
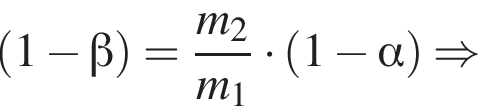
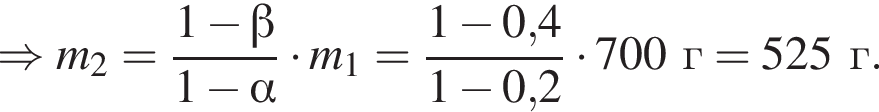
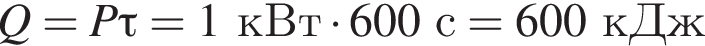 энергии.
энергии. 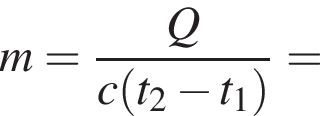
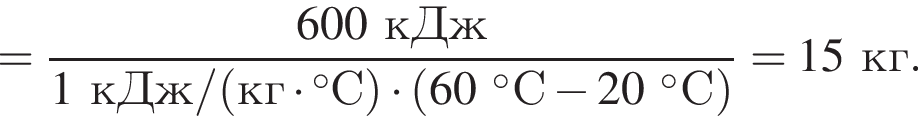
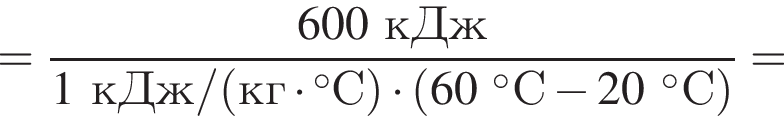
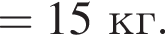

 И значит:
И значит: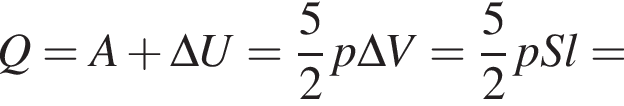
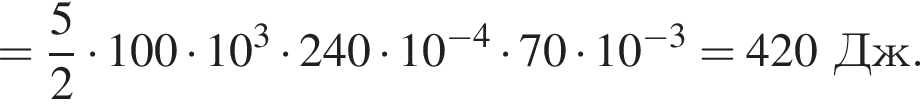
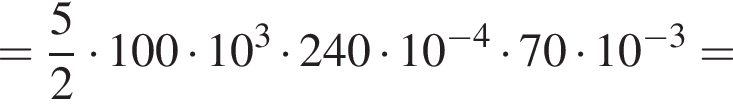
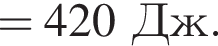

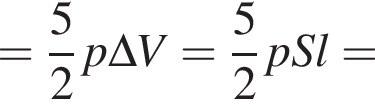
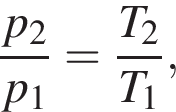 при этом
при этом 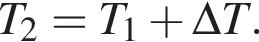 Тогда получаем:
Тогда получаем: 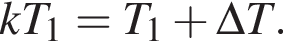 Откуда начальная температура газа
Откуда начальная температура газа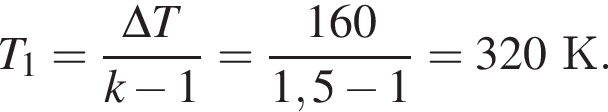
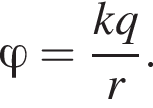 Из рисунка видно, что растояние между точками равно
Из рисунка видно, что растояние между точками равно 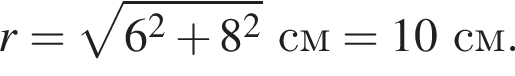 Потенциал в точке B равен
Потенциал в точке B равен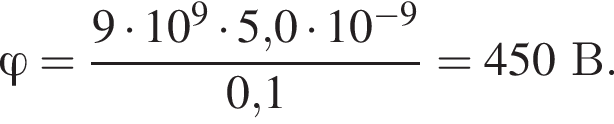
 Под действием этой силы частица дdижется по кругу, т. е. приобретает центростремительное ускорение:
Под действием этой силы частица дdижется по кругу, т. е. приобретает центростремительное ускорение: 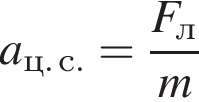 или
или 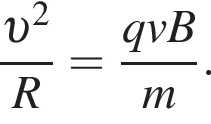 Выразим отсюда индукцию магнитного поля
Выразим отсюда индукцию магнитного поля 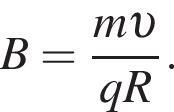 Поскольку ионы находится в одном и том же поле, можно записать:
Поскольку ионы находится в одном и том же поле, можно записать: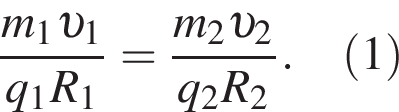
 Из рисунка видно, что
Из рисунка видно, что 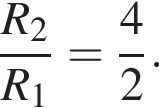 За одно и тоже время первый ион прошёл путь
За одно и тоже время первый ион прошёл путь 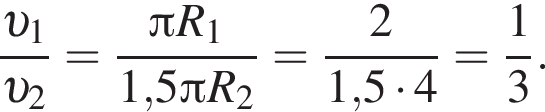
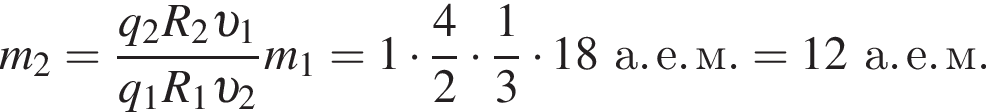
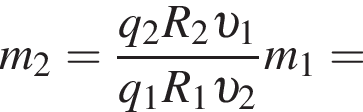
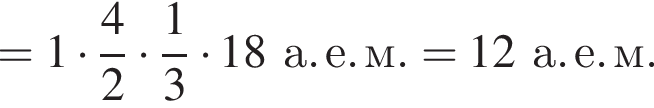

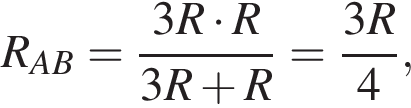 откуда
откуда 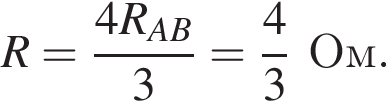
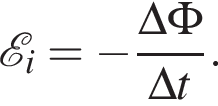 По закону Ома для полной цепи сила индукционного тока равна
По закону Ома для полной цепи сила индукционного тока равна 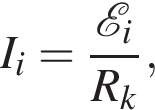 где сопротивление контура равняется
где сопротивление контура равняется 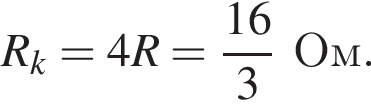 Следовательно, сила тока в цепи равна
Следовательно, сила тока в цепи равна 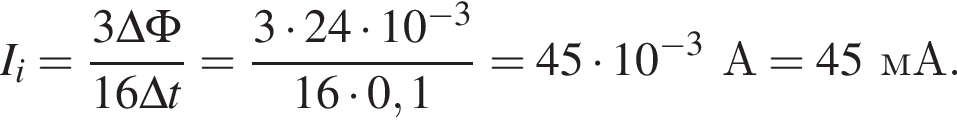
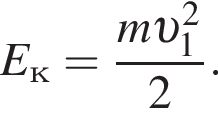 В электрическом поле шарик разгоняется, увеличивая свою кинетическую энергию на
В электрическом поле шарик разгоняется, увеличивая свою кинетическую энергию на  В установившемся режиме после соударения с противоположной пластиной кинетическая энергия шарика уменьшается до исходного значения
В установившемся режиме после соударения с противоположной пластиной кинетическая энергия шарика уменьшается до исходного значения 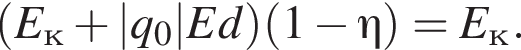
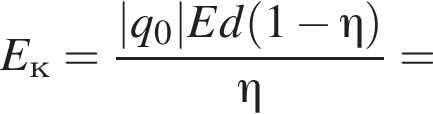
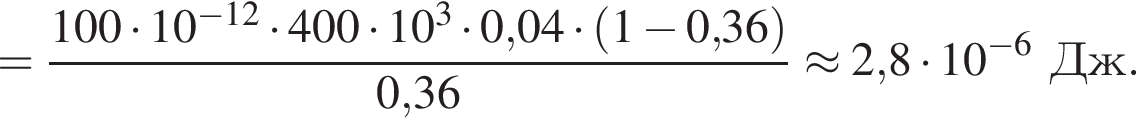
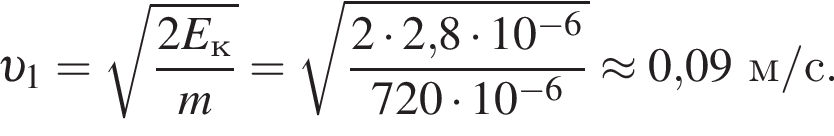
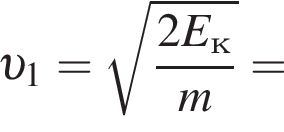
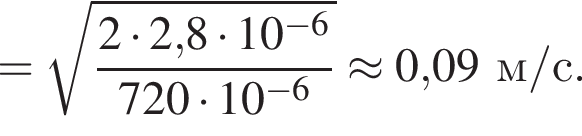
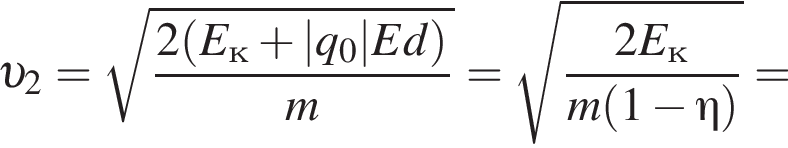
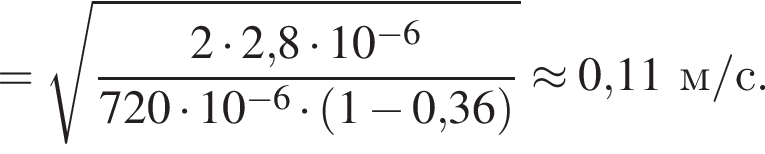
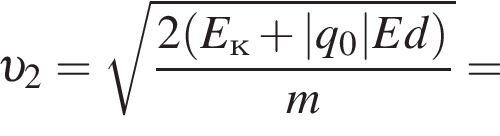
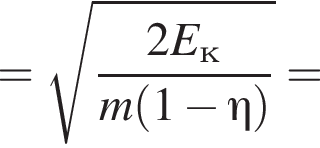
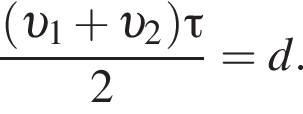
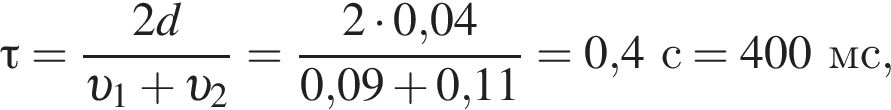
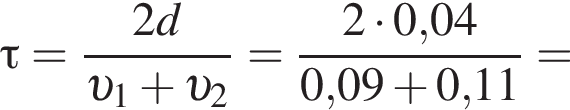


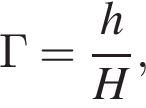 откуда
откуда 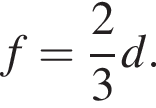
 Тогда расстояние от предмета до линзы равно
Тогда расстояние от предмета до линзы равно 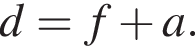 Тогда получим, что
Тогда получим, что 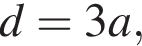
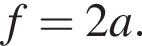
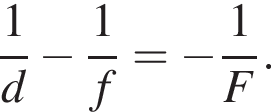
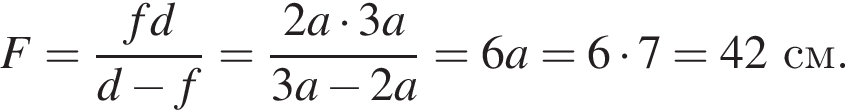
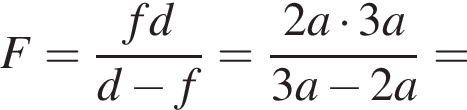
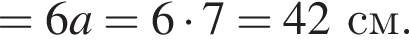
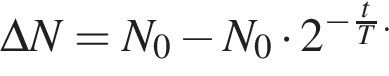
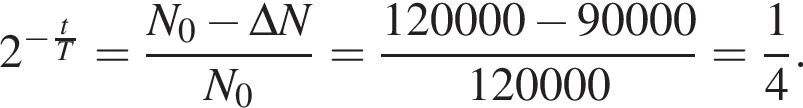
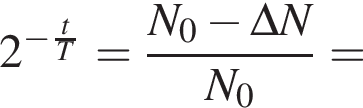
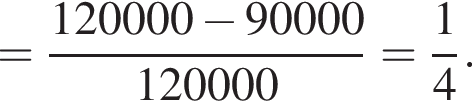

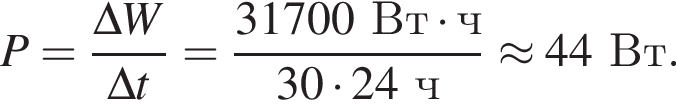
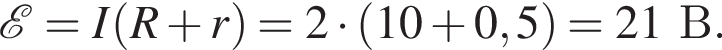
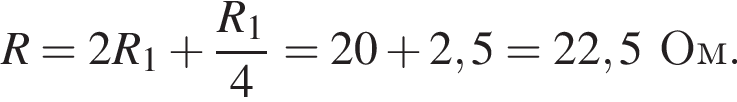
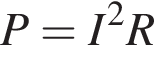 найдем силу тока через шестой резистор:
найдем силу тока через шестой резистор: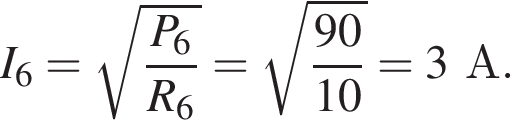
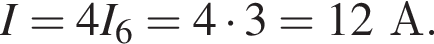 По закону Ома для полной цепи ЭДС источника тока равна
По закону Ома для полной цепи ЭДС источника тока равна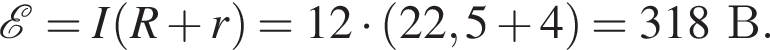
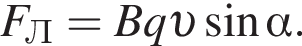 Поскольку электрон движется по окружности, то
Поскольку электрон движется по окружности, то 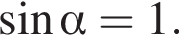 Тогда модуль индукции магнитного поля равен
Тогда модуль индукции магнитного поля равен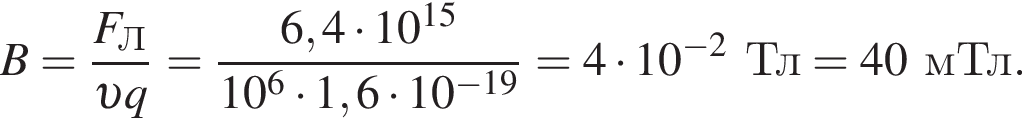
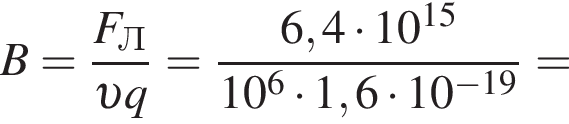
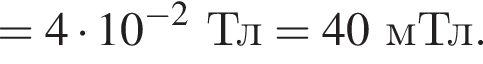
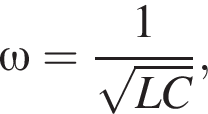 откуда находим емкость конденсатора:
откуда находим емкость конденсатора: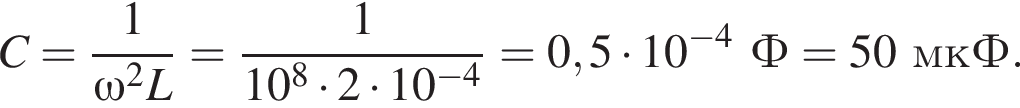
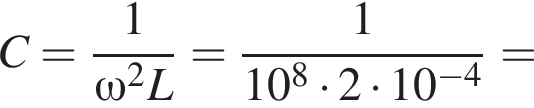
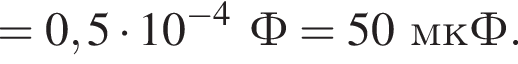
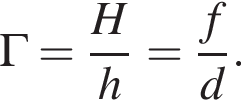 Объединяя уравнения, получаем:
Объединяя уравнения, получаем: 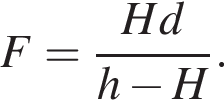 Учитывая, что размер карандаша не меняется, запишем систему уравнений для двух точек графика:
Учитывая, что размер карандаша не меняется, запишем систему уравнений для двух точек графика: